| Copyright | (c) 2013-2015 2021 Jean-Luc JOULIN |
|---|---|
| License | Private |
| Maintainer | jean-luc-joulin@orange.fr |
| Stability | experimental |
| Portability | portable |
| Safe Haskell | None |
| Language | Haskell98 |
HsMesher.Algorithms1D.Segments
Contents
Description
Les algorithmes de générations des noeuds pour des segments droits.
Synopsis
- meshSegment :: (Enum a, Integral a, Enum b, RealFloat b) => (b, b, b) -> (b, b, b) -> MeshingMethod1D a b -> MeshingResult1D b
- correctSpa :: (Enum a, Integral a, Enum b, RealFloat b) => a -> b -> b
Documentation
La fonction principale de maillage des segments de droite est meshSegment.
Cette fonction permet de générer des noeuds sur un segment de droite avec les différentes
méthodes MeshingMethod1D.
>>>meshSegment (0,0,0) (10,10,0) (NdivRegular 3)Mesh1D [(0.0,0.0,0.0),(3.3333333333333335,3.3333333333333335,0.0),(6.666666666666667,6.666666666666667,0.0),(10.0,10.0,0.0)]
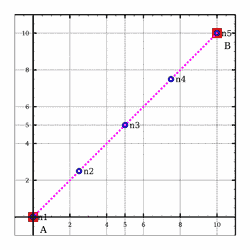
>>>meshSegment (0,0,0) (10,10,0) (NdivRegular 4)Mesh1D [(0.0,0.0,0.0),(2.5,2.5,0.0),(5.0,5.0,0.0),(7.5,7.5,0.0),(10.0,10.0,0.0)]
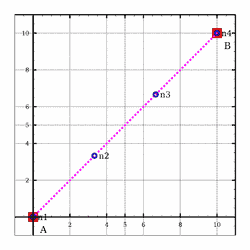
Meshing_Test_1D_Odd_Segment_NdivRegular1_3
Meshing_Test_1D_Even_Segment_NdivRegular1_4
>>>meshSegment (0,0,0) (10,10,0) (NdivRegular 9)Mesh1D [(0.0,0.0,0.0),(1.1111111111111112,1.1111111111111112,0.0),(2.2222222222222223,2.2222222222222223,0.0),(3.3333333333333335,3.3333333333333335,0.0),(4.444444444444445,4.444444444444445,0.0),(5.555555555555555,5.555555555555555,0.0),(6.666666666666667,6.666666666666667,0.0),(7.777777777777779,7.777777777777779,0.0),(8.88888888888889,8.88888888888889,0.0),(10.0,10.0,0.0)]
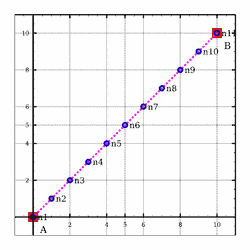
>>>meshSegment (0,0,0) (10,10,0) (NdivRegular 10)Mesh1D [(0.0,0.0,0.0),(1.0,1.0,0.0),(2.0,2.0,0.0),(3.0,3.0,0.0),(4.0,4.0,0.0),(5.0,5.0,0.0),(6.0,6.0,0.0),(7.0,7.0,0.0),(8.0,8.0,0.0),(9.0,9.0,0.0),(10.0,10.0,0.0)]
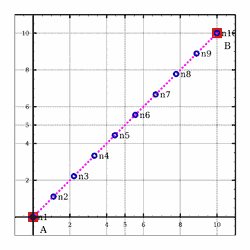
Meshing_Test_1D_Odd_Segment_NdivRegular1_9
Meshing_Test_1D_Even_Segment_NdivRegular1_10
>>>meshSegment (0,0,0) (10,10,0) (NdivLinear 9 5)Mesh1D [(0.0,0.0,0.0),(0.37037037037037035,0.37037037037037035,0.0),(0.9259259259259259,0.9259259259259259,0.0),(1.6666666666666667,1.6666666666666667,0.0),(2.5925925925925926,2.5925925925925926,0.0),(3.7037037037037037,3.7037037037037037,0.0),(5.0,5.0,0.0),(6.481481481481482,6.481481481481482,0.0),(8.148148148148149,8.148148148148149,0.0),(10.0,10.0,0.0)]
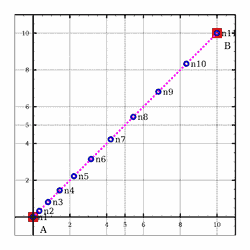
>>>meshSegment (0,0,0) (10,10,0) (NdivLinear 10 5)Mesh1D [(0.0,0.0,0.0),(0.3333333333333333,0.3333333333333333,0.0),(0.8148148148148148,0.8148148148148148,0.0),(1.4444444444444446,1.4444444444444446,0.0),(2.2222222222222223,2.2222222222222223,0.0),(3.148148148148148,3.148148148148148,0.0),(4.222222222222222,4.222222222222222,0.0),(5.444444444444445,5.444444444444445,0.0),(6.814814814814815,6.814814814814815,0.0),(8.333333333333334,8.333333333333334,0.0),(10.0,10.0,0.0)]
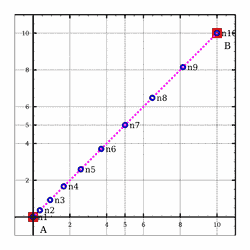
Meshing_Test_1D_Odd_Segment_NdivLinear1_9_5
Meshing_Test_1D_Even_Segment_NdivLinear1_10_5
>>>meshSegment (0,0,0) (10,10,0) (NdivLinear 9 0.2)Mesh1D [(0.0,0.0,0.0),(1.851851851851852,1.851851851851852,0.0),(3.518518518518519,3.518518518518519,0.0),(5.000000000000001,5.000000000000001,0.0),(6.296296296296297,6.296296296296297,0.0),(7.407407407407407,7.407407407407407,0.0),(8.333333333333334,8.333333333333334,0.0),(9.074074074074076,9.074074074074076,0.0),(9.62962962962963,9.62962962962963,0.0),(10.0,10.0,0.0)]
>>>meshSegment (0,0,0) (10,10,0) (NdivLinear 10 0.2)Mesh1D [(0.0,0.0,0.0),(1.6666666666666667,1.6666666666666667,0.0),(3.185185185185185,3.185185185185185,0.0),(4.555555555555555,4.555555555555555,0.0),(5.777777777777778,5.777777777777778,0.0),(6.851851851851852,6.851851851851852,0.0),(7.777777777777778,7.777777777777778,0.0),(8.555555555555557,8.555555555555557,0.0),(9.185185185185185,9.185185185185185,0.0),(9.666666666666666,9.666666666666666,0.0),(10.0,10.0,0.0)]
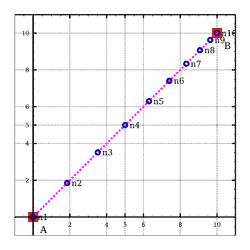
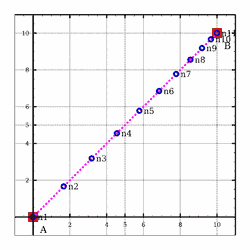
Meshing_Test_1D_Odd_Segment_NdivLinear1_9_0.2
Meshing_Test_1D_Even_Segment_NdivLinear1_10_0.2
>>>meshSegment (0,0,0) (10,10,0) (NdivDoubleLinear 9 5)Mesh1D [(0.0,0.0,0.0),(0.5714285714285714,0.5714285714285714,0.0),(1.3571428571428572,1.3571428571428572,0.0),(2.357142857142857,2.357142857142857,0.0),(3.5714285714285716,3.5714285714285716,0.0),(6.428571428571429,6.428571428571429,0.0),(7.642857142857142,7.642857142857142,0.0),(8.642857142857142,8.642857142857142,0.0),(9.428571428571429,9.428571428571429,0.0),(10.0,10.0,0.0)]
>>>meshSegment (0,0,0) (10,10,0) (NdivDoubleLinear 10 5)Mesh1D [(0.0,0.0,0.0),(0.3333333333333333,0.3333333333333333,0.0),(1.0,1.0,0.0),(2.0,2.0,0.0),(3.333333333333333,3.333333333333333,0.0),(5.0,5.0,0.0),(6.666666666666667,6.666666666666667,0.0),(8.0,8.0,0.0),(9.0,9.0,0.0),(9.666666666666668,9.666666666666668,0.0),(10.0,10.0,0.0)]
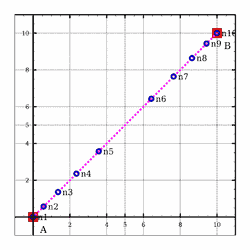
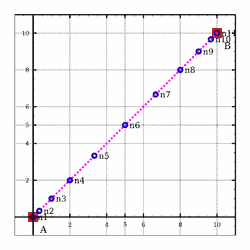
Meshing_Test_1D_Odd_Segment_NdivDoubleLinear1_9_5
Meshing_Test_1D_Even_Segment_NdivDoubleLinear1_10_5
>>>meshSegment (0,0,0) (10,10,0) (NdivDoubleLinear 9 0.2)Mesh1D [(0.0,0.0,0.0),(1.8181818181818181,1.8181818181818181,0.0),(3.227272727272727,3.227272727272727,0.0),(4.227272727272727,4.227272727272727,0.0),(4.818181818181818,4.818181818181818,0.0),(5.181818181818182,5.181818181818182,0.0),(5.7727272727272725,5.7727272727272725,0.0),(6.7727272727272725,6.7727272727272725,0.0),(8.181818181818182,8.181818181818182,0.0),(10.0,10.0,0.0)]
>>>meshSegment (0,0,0) (10,10,0) (NdivDoubleLinear 10 0.2)Mesh1D [(0.0,0.0,0.0),(1.6666666666666667,1.6666666666666667,0.0),(3.0,3.0,0.0),(4.0,4.0,0.0),(4.666666666666667,4.666666666666667,0.0),(5.0,5.0,0.0),(5.333333333333333,5.333333333333333,0.0),(6.0,6.0,0.0),(7.0,7.0,0.0),(8.333333333333332,8.333333333333332,0.0),(10.0,10.0,0.0)]
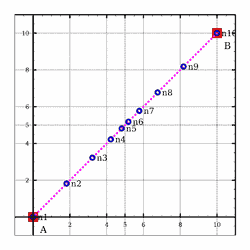
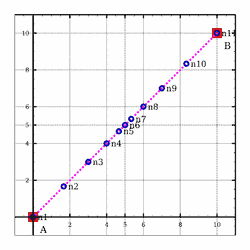
Meshing_Test_1D_Odd_Segment_NdivDoubleLinear1_9_0.2
Meshing_Test_1D_Even_Segment_NdivDoubleLinear1_10_0.2
>>>meshSegment (0,0,0) (10,10,0) (NdivRegular 0)NegativeSizing
>>>meshSegment (10,10,0) (10,10,0) (NdivRegular 4)CoincidentsPoints (10.0,10.0,0.0) (10.0,10.0,0.0)
Arguments
| :: (Enum a, Integral a, Enum b, RealFloat b) | |
| => (b, b, b) | Les coordonnées du premier point du segment |
| -> (b, b, b) | Les coordonnées du deuxième point du segment |
| -> MeshingMethod1D a b | La méthode de maillage du segment |
| -> MeshingResult1D b | Le résultat du maillage |
Fonction annexe
correctSpa :: (Enum a, Integral a, Enum b, RealFloat b) => a -> b -> b #
Corrige les valeurs de ratio pour la méthode NdivDoubleLinear.
Lorsqu'un élément est maillé avec une valeur de division impaire, le maillage est
généré avec un ratio inférieur a celui attendu. La fonction correctSpa permet
de corriger ce problème avec une formule obtenue experimentalement.
Les ratios mesurés en fonction du ratio introduit donnent les courbes ci-dessous
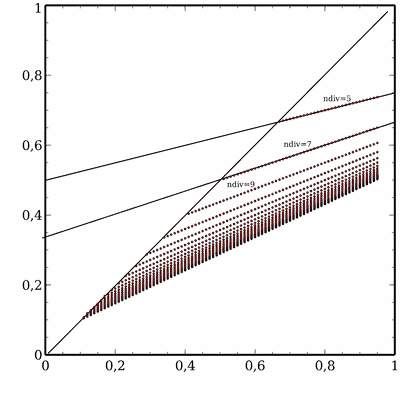
On remarque qu'au dessus d'un certain ratio et en fonction du nombre de divisions les courbes changent de pente et s'applatissent.
L'analyse mathématique montre que l'équation de ces courbes aplanies est:
space_mesure = (spac_theorique - (2 / (ndiv - 1))) / ((0.5 * ndiv - 1.5) / (ndiv - 1))
et que la limite a partir de laquelle elle est valable est:
spac < (4 / (ndiv + 1))